In plant breeding programmes multi-environment trials (MET) form the backbone for phenotypic selection, Genomic Selection (GS) and Genome Wide Association Study (GWAS). Efficient analysis of MET is fundamental to get accurate results from phenotypic selection, GS and GWAS.
On the other hand inefficient analysis of MET data may have consequences such as biased ranking of genotype means in phenotypic data analysis, small accuracy of GS and wrong identification of QTL in GWAS analysis. A combined analysis of MET is performed using either single-stage or stage-wise (two-stage) approaches based on the linear mixed model framework. While single-stage analysis is a fully efficient approach, MET data is suitably analyzed using stage-wise methods. MET data often show within-trial and between-trial variance heterogeneities, which is in contradiction with the homogeneity of variance assumption of linear models, and these heterogeneities require corrections. In addition it is well documented that spatial correlations are inherent to most field trials. Appropriate remedial techniques for variance heterogeneities and proper accounting of spatial correlation are useful to improve accuracy and efficiency of MET analysis.
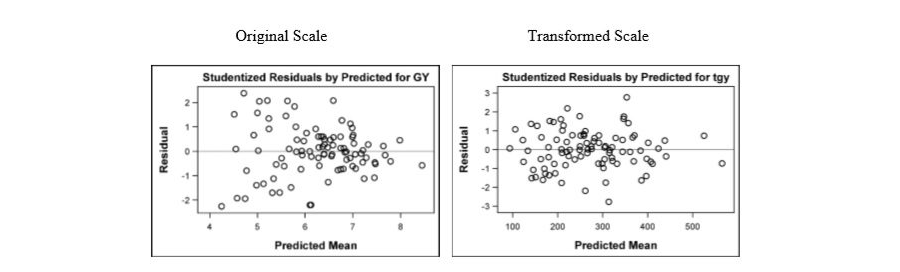
The study conducted based on three maize trials from Ethiopia compares methods for simultaneous handling of within-trial variance heterogeneity and within-trial spatial correlation. To stabilize variance Box-Cox transformation was considered. The result shows that, while the Box-Cox transformation was suitable for stabilizing the variance, it is difficult to report results on the original scale. As alternative variance models, i.e. power-of-the-mean (POM) and exponential models, were used to fix the variance heterogeneity problem. Unlike the Box-Cox method, the variance models considered in this study were successful to deal simultaneously with both spatial correlation and heterogeneity of variance.
The study shows that stage-wise analysis is a suitable approach for practical analysis of MET, GS and GWAS analysis. Single-stage and two-stage analysis of MET yield very similar results. Stage-wise analysis can be nearly as efficient as single-stage analysis when using optimal weighting, i.e., fully-efficient weighting. Spatial variation and within-trial variance heterogeneity are common in MET data.